宅男小C
Time Limit: 10 Sec Memory Limit: 256 MB
Description
众所周知,小C是个宅男,所以他的每天的食物要靠外卖来解决。小C现在有M元钱,他想知道这些钱他最多可以吃多少天。
餐厅提供N种食物,每种食物有两个属性,单价Pi和保质期Si,表示小C需要花Pi元才能买到足够一天吃的这种食物,并且需要在送到Si天内吃完,否则食物会变质,就不能吃了,若Si为0则意味着必须在送到当天吃完。另外,每次送餐需要额外F元送餐费。
每个测试点包含多组测试数据;
每个测试数据第一行三个整数M,F,N,如题目描述中所述;
以下N行,每行两个整数,分别表示Pi和*Si。*
Output
对于每个测试数据输出一行,表示最多可以吃的天数。
32 5 2
5 0
10 2
10 10 1
10 10
10 1 1
1 5
Sample Output
3
0
8
HINT
对于40%的数据,M,Si <= 2*10^6;
对于100%的数据,1 ≤ N ≤ 200,M, Si<= 10^18,1 ≤ T ≤ 50,1 ≤ F ≤ M,1 ≤ Pi ≤ M。
Main idea
每种食物有一个花费和一个保质期,在保质期内食用可以多活一天,每次购买可以买多个食物,买一次会耗费一些钱,问最多能活几天。
Solution
我们先从简单的做法入手,如果确定了购买次数,能求出最多活几天吗?答案是显然可以的。我们运用贪心:首先,若存在某种价格又贵保质期又短的食物显然是没有用的,我们sort一遍直接删去,然后我们可以得到一个价格上升且保质期上升的序列。我们基于这里开始贪心:我们先从便宜的食物入手,显然每次都是从这种食物吃起,仅存在两种不购买便宜的情况:1.保质期过了;2.钱不够满足所有次数了。如果保质期过了,我们就选择下一个食物,如果钱不够满足所有次数了,那就能买几次买几次,记录一下答案,退出。
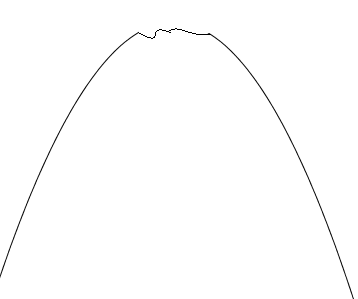
我们解决了确定购买次数最多活几天之后,再仔细思考:由于购买会花钱,那么我们大胆猜测购买次数和活的天数有一定的规律,我们画了几张图之后,发现其比例大致单峰,如下图所示:

我们发现,显然中间有一段波动,那么就不能使用三分法了。那怎么办呢?但是我们再发现:函数最后波动段非常短!显然在随机范围内可行,那么显然我们可以使用随机化算法!这里我们运用模拟退火。直接模拟退火随机一个购买次数,然后Judge更新即可。
随机化算法是坠吼的!(≧▽≦)/
Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
| #include<bits/stdc++.h>
using namespace std;
typedef long long s64;
const int ONE = 10005;
const int INF = 2147483640;
int n;
s64 A,Now,Ans;
s64 Total,F;
struct power
{
s64 cost;
s64 days;
}a[ONE];
bool cmp(const power &a,const power &b)
{
if(a.cost == b.cost) return a.days > b.days;
return a.cost < b.cost;
}
int get()
{
int res=1,Q=1; char c;
while( (c=getchar())<48 || c>57)
if(c=='-')Q=-1;
if(Q) res=c-48;
while((c=getchar())>=48 && c<=57)
res=res*10+c-48;
return res*Q;
}
void pre()
{
sort(a+1,a+n+1,cmp); s64 d=-1;
int m=n; n=0;
for(int i=1;i<=m;i++)
if(a[i].days > d)
a[++n]=a[i], d=a[i].days;
}
s64 Judge(s64 times)
{
if(times<=0) return 0;
s64 Money = Total - times * F;
s64 res = 0, num, day = 0;
for(int i=1;i<=n;i++)
{
num = min(Money / a[i].cost / times, a[i].days - day + 1);
Money -= num * a[i].cost * times;
day += num; res += times * num;
if(day <= a[i].days)
{
num = Money / a[i].cost;
res += num;
Ans = max(Ans, res);
return res;
}
}
Ans = max(Ans, res);
return res;
}
double Random() {return rand()/(double)RAND_MAX;}
void SA(double T)
{
Now = 1;
while(T >= 1)
{
A = Now + (s64)(T * (Random()*2-1)) ;
if(A<=0) A = T*Random();
s64 dE = Judge(A) - Judge(Now);
if(dE > 0)
Now = A;
T *= 0.93;
}
}
void Solve()
{
for(int i=1;i<=n;i++)
scanf("%lld %lld",&a[i].cost,&a[i].days);
pre();
Ans = 0;
SA(Total / F + 1);
printf("%lld\n",Ans);
}
int main()
{
while(scanf("%lld %lld %d",&Total,&F,&n) != EOF)
Solve();
}
|