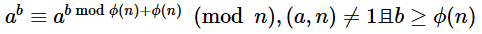相逢是问候
Time Limit: 40 Sec Memory Limit: 512 MB
Description
Informatikverbindetdichundmich.
信息将你我连结。B君希望以维护一个长度为n的数组,这个数组的下标为从1到n的正整数。一共有m个操作,可以
分为两种:0 l r表示将第l个到第r个数(al,al+1,…,ar)中的每一个数ai替换为c^ai,即c的ai次方,其中c是
输入的一个常数,也就是执行赋值ai=c^ai1 l r求第l个到第r个数的和,也就是输出:sigma(ai),l<=i<=rai因为
这个结果可能会很大,所以你只需要输出结果mod p的值即可。
第一行有三个整数n,m,p,c,所有整数含义见问题描述。
接下来一行n个整数,表示a数组的初始值。
接下来m行,每行三个整数,其中第一个整数表示了操作的类型。
如果是0的话,表示这是一个修改操作,操作的参数为l,r。
如果是1的话,表示这是一个询问操作,操作的参数为l,r。
Output
对于每个询问操作,输出一行,包括一个整数表示答案mod p的值。
4 4 7 2
1 2 3 4
0 1 4
1 2 4
0 1 4
1 1 3
Sample Output
0
3
HINT
1 ≤ n ≤ 50000, 1 ≤ m ≤ 50000, 1 ≤ p ≤ 100000000, 0 < c <p, 0 ≤ ai < p
Solution
首先,我们运用欧拉定理:

然后还有一个定理:一个数在执行log次操作后,值不会改变。
于是乎,我们可以运用线段树,暴力修改每一个值,如果值都不变了则不修改。
然后我们再考虑一下,怎么修改这个值:
已知a(原值)和times(修改次数),我们考虑每一次%什么,
考虑每一次b的模数。
首先如果b%phi§,意味着a^b在**%p下同余。
如果这一次b%phi(phi§),意味着a^b在phi§下同余,
同时也意味着下一次在%phi§意义下。
我们要让答案最后是在%p意义下的,那么显然每次b%phi[times-1]。
再带上快速幂,那么这样效率就是O(nlog^3(n))**的。
Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
| #include<bits/stdc++.h>
using namespace std;
typedef long long s64;
const int ONE = 500005;
const int INF = 2147483640;
int n,m,p,C;
int opt,x,y;
int a[ONE],phi[ONE],p_num;
int MOD;
int res;
struct power
{
int value;
int cnt;
}Node[ONE];
int get()
{
int res=1,Q=1;char c;
while( (c=getchar())<48 || c>57 )
if(c=='-')Q=-1;
res=c-48;
while( (c=getchar())>=48 && c<=57 )
res=res*10+c-48;
return res*Q;
}
int Getphi(int n)
{
int res = n;
for(int i=2; i*i<=n; i++)
if(n % i == 0)
{
res = res/i*(i-1);
while(n % i == 0) n /= i;
}
if(n != 1) res = res/n*(n-1);
return res;
}
int Quickpow(int a,int b,int MOD)
{
int res = 1;
while(b)
{
if(b & 1) res = (s64)res * a % MOD;
a = (s64)a * a % MOD;
b >>= 1;
}
return res;
}
void Build(int i,int l,int r)
{
if(l == r)
{
Node[i].value = a[l] % MOD;
return;
}
int mid = l+r>>1;
Build(i<<1, l, mid);
Build(i<<1|1, mid + 1, r);
Node[i].value = (Node[i<<1].value + Node[i<<1|1].value) % MOD;
}
int Calc(int a, int times)
{
for(int i=times; i>=1; i--)
{
if(a >= phi[i]) a = a%phi[i] + phi[i];
a = Quickpow(C, a, phi[i-1]);
if(!a) a = phi[i-1];
}
return a;
}
void Update(int i,int l,int r,int L,int R)
{
if(Node[i].cnt >= p_num) return;
if(l == r)
{
Node[i].value = Calc(a[l], ++Node[i].cnt);
return;
}
int mid = l+r>>1;
if(L <= mid) Update(i<<1, l, mid, L, R);
if(mid+1 <= R) Update(i<<1|1, mid+1, r, L, R);
Node[i].value = (Node[i<<1].value + Node[i<<1|1].value) % MOD;
Node[i].cnt = min(Node[i<<1].cnt, Node[i<<1|1].cnt);
}
void Query(int i,int l,int r,int L,int R)
{
if(L<=l && r<=R)
{
res = (res + Node[i].value) % MOD;
return;
}
int mid = l+r>>1;
if(L <= mid) Query(i<<1, l, mid, L, R);
if(mid+1 <= R) Query(i<<1|1, mid+1, r, L, R);
}
int main()
{
n = get(); m = get(); p = get(); C = get();
for(int i=1; i<=n; i++) a[i] = get();
MOD = phi[0] = p;
while(p!=1) phi[++p_num] = p = Getphi(p);
phi[++p_num] = 1;
Build(1, 1, n);
while(m--)
{
opt = get();
x = get(); y = get();
if(!opt) Update(1, 1, n, x, y);
else
{
res = 0;
Query(1, 1, n, x, y);
printf("%d\n", res);
}
}
}
|