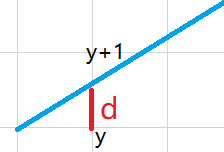基础图形绘制-直线

DDA

数值微分 DDA (Digital Differential Analyzer) 算法

给点两点 (x1,y1)、(x2,y2)(x_1,y_1)、(x_2,y_2) ，考虑直线表达式： y=kx+b,k=y2−y1x2−x1y=kx+b,k=\frac{y2-y1}{x2-x1}

显然我们可以直接模拟这个过程：从 (x1,y1)(x_1,y_1) 走向 (x2,y2)(x_2, y_2)，每次 x+1x+1 的时候 y+ky+k。

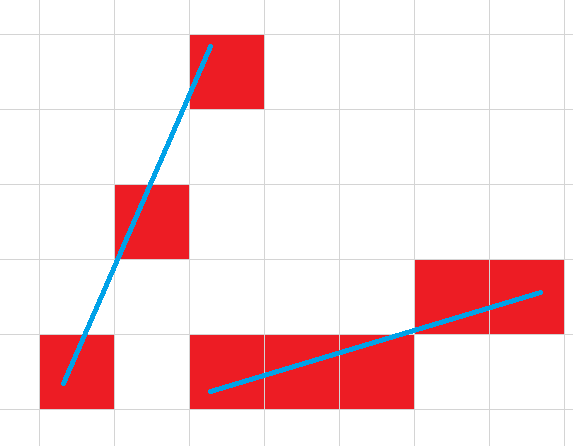
易发现，在斜率 kk 较小的时候，所画直线比较合理，但是在 kk 比较大的时候，会出现下图左侧这样割裂的问题：

image-20210923210159313

于是，我们在 kk 较大的时候，交换表达式中的 xx 、yy，这样就可以让 kk 变小。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
static void Normalize(float &x, float &y)
{
	x = (x - (SCR_WIDTH / 2)) / (SCR_WIDTH / 2);
	y = (y - (SCR_HEIGHT / 2)) / (SCR_HEIGHT / 2);
}

static void DDA(int x1, int y1, int x2, int y2)
{
	int dx = x2 - x1, dy = y2 - y1;
	int _k = abs(dx) > abs(dy) ? abs(dx) : abs(dy);

	float x = x1, y = y1;
	for (int i = 0; i <= _k; i++, count++)
	{
		vertices[i * 3] = x, x += (float)dx / _k;
		vertices[i * 3 + 1] = y, y += (float)dy / _k;

		Normalize(vertices[i * 3], vertices[i * 3 + 1]);
	}
}

Bresenham

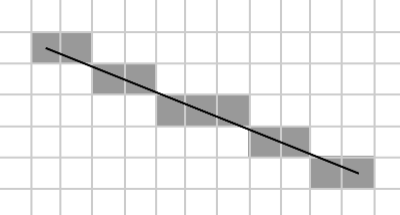
Bresenham 算法是计算机图形学典型的直线光栅化算法。

image-20210923212851571

假设 k∈[0,1]k \in [0,1]，在绘制一条直线的时候，我们考虑每次将 x+1x+1，那么对于一个点 (x,y)(x,y)，理想的下一个点应该是 (x+1,y+k),k=y2−y1x2−x1(x+1,y+k),k=\frac{y_2-y_1}{x_2-x_1}。

但我们栅格化后，绘制的下一个点是 (x+1,y)(x+1,y) 或 (x+1,y+1)(x+1,y+1)，于是考虑应该选择哪个点。

我们令 dd 表示从 yy 到理想位置的误差，显然有 d∈[0,1)d\in[0,1) ：

image-20210923213153789

显然，当 d≤0.5d\le0.5 时，我们选择 (x+1,y)(x+1,y) ；当 d>0.5d\gt0.5 时，我们选择 (x+1,y+1)(x+1,y+1)。

首先：考虑怎么求这个 dd，显然设 dd 的初值为 00；每次 x+1x+1 时候，d+k,k=ΔyΔxd+k,k=\frac{\Delta y}{\Delta x} ；若 d>0.5d\gt0.5，yy 变成了 y+1y+1，相对的也要 d−1d-1 ，保证其相对性。

现在有：

xi+1=xi+1yi+1={yiif d≤0.5yi+1if d>0.5d0=0di+1=di+ΔyΔxd=d−1   if d>0.5x_{i+1} = x_{i} + 1\\ y_{i+1} = \begin{cases} y_{i} & \text{if $d \leq 0.5$} \\ y_{i}+1 & \text{if $d \gt 0.5$} \end{cases}\\ d_0=0\\ d_{i+1}=d_i+\frac{\Delta y}{\Delta x}\\ d=d-1 \:\:\: \text{if $d \gt 0.5$}

我们考虑优化一下这个式子，去掉精度处理：

  1. 令 d=d−0.5d=d-0.5，得到：

xi+1=xi+1yi+1={yiif d≤0yi+1if d>0d0=−0.5di+1=di+ΔyΔxd=d−1   if d>0x_{i+1} = x_{i} + 1\\ y_{i+1} = \begin{cases} y_{i} & \text{if $d \leq 0$} \\ y_{i}+1 & \text{if $d \gt 0$} \end{cases}\\ d_0=-0.5\\ d_{i+1}=d_i+\frac{\Delta y}{\Delta x}\\ d=d-1 \:\:\: \text{if $d \gt 0$}

  1. 令 d=d×2×Δxd=d \times 2 \times \Delta x，得到：

xi+1=xi+1yi+1={yiif d≤0yi+1if d>0d0=−Δxdi+1=di+2×Δyd=d−2×Δx   if d>0x_{i+1} = x_{i} + 1\\ y_{i+1} = \begin{cases} y_{i} & \text{if $d \leq 0$} \\ y_{i}+1 & \text{if $d \gt 0$} \end{cases}\\ d_0=-\Delta x\\ d_{i+1}=d_i+2\times\Delta y\\ d=d-2 \times \Delta x \:\:\: \text{if $d \gt 0$}

这样就可以实现 k∈[0,1]k \in [0,1] 的直线的绘制。

最后，我们扩展一下，处理一下其它情况即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
static void Normalize(float &x, float &y)
{
	x = (x - (SCR_WIDTH / 2)) / (SCR_WIDTH / 2);
	y = (y - (SCR_HEIGHT / 2)) / (SCR_HEIGHT / 2);
}

static void swap(int& a, int& b) { int temp = a; a = b; b = temp; }

static void Bresenham(int x1, int y1, int x2, int y2)
{
	bool steep = abs(y2 - y1) > abs(x2 - x1);
	if (steep) swap(x1, y1), swap(x2, y2);
	if (x1 > x2) swap(x1, x2), swap(y1, y2);
	int dx = x2 - x1, dy = y2 - y1;

    int d = -dx;
	for (int i = 0, x = x1, y = y1; i <= dx; i++, count++)
	{
        vertices[i * 3] = !steep ? x : y;
		vertices[i * 3 + 1] = !steep ? y : x;

		Normalize(vertices[i * 3], vertices[i * 3 + 1]);

        x++;
		d += 2 * abs(dy);
        if (d > 0) y += (dy > 0 ? 1 : -1), d -= 2 * dx;
	}
}

OpenGL 完整代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
#define GLEW_STATIC
#include <GL/glew.h>
#include <GL/GL.h>
#include <GLFW/glfw3.h>

#include <iostream>

#pragma region Setting

static GLFWwindow* window;
const unsigned int SCR_WIDTH = 800;
const unsigned int SCR_HEIGHT = 600;
const unsigned int MAX_COUNT = 800 * 600;

static void InitializeWindow()
{
	glfwInit();
	glfwWindowHint(GLFW_CONTEXT_VERSION_MAJOR, 3);
	glfwWindowHint(GLFW_CONTEXT_VERSION_MINOR, 3);
	glfwWindowHint(GLFW_OPENGL_PROFILE, GLFW_OPENGL_CORE_PROFILE);

	window = glfwCreateWindow(SCR_WIDTH, SCR_HEIGHT, "Test", NULL, NULL);
	glfwMakeContextCurrent(window);
	glfwSetFramebufferSizeCallback(window, [](GLFWwindow* window, int width, int height){ glViewport(0, 0, width, height); });


	glewExperimental = GL_TRUE;
	glewInit();

}

static void ProcessInput(GLFWwindow* window)
{
	if (glfwGetKey(window, GLFW_KEY_ESCAPE) == GLFW_PRESS)
		glfwSetWindowShouldClose(window, true);
}
#pragma endregion


#pragma region InitializeVertex

static float vertices[MAX_COUNT * 3];
static unsigned int VAO, VBO;
static unsigned int count = 0;

static void Normalize(float& x, float& y)
{
	x = (x - (SCR_WIDTH / 2)) / (SCR_WIDTH / 2);
	y = (y - (SCR_HEIGHT / 2)) / (SCR_HEIGHT / 2);
}

static void DDA(int x1, int y1, int x2, int y2)
{
	int dx = x2 - x1, dy = y2 - y1;
	int _k = abs(dx) > abs(dy) ? abs(dx) : abs(dy);

	float x = x1, y = y1;
	for (int i = 0; i <= _k; i++, count++)
	{
		vertices[i * 3] = x, x += (float)dx / _k;
		vertices[i * 3 + 1] = y, y += (float)dy / _k;

		Normalize(vertices[i * 3], vertices[i * 3 + 1]);
	}
}

static void swap(int& a, int& b) { int temp = a; a = b; b = temp; }

static void Bresenham(int x1, int y1, int x2, int y2)
{
	bool steep = abs(y2 - y1) > abs(x2 - x1);
	if (steep) swap(x1, y1), swap(x2, y2);
	if (x1 > x2) swap(x1, x2), swap(y1, y2);
	int dx = x2 - x1, dy = y2 - y1;

    int d = -dx;
	for (int i = 0, x = x1, y = y1; i <= dx; i++, count++)
	{
        vertices[i * 3] = !steep ? x : y;
		vertices[i * 3 + 1] = !steep ? y : x;

		Normalize(vertices[i * 3], vertices[i * 3 + 1]);

        x++;
		d += 2 * abs(dy);
        if (d > 0) y += (dy > 0 ? 1 : -1), d -= 2 * dx;
	}
}


static void InitializeVertex()
{
	// Generate
	glGenVertexArrays(1, &VAO);
	glGenBuffers(1, &VBO);

	// Bind
	glBindVertexArray(VAO);
	glBindBuffer(GL_ARRAY_BUFFER, VBO);

	glBufferData(GL_ARRAY_BUFFER, sizeof(vertices), vertices, GL_STATIC_DRAW);

	glVertexAttribPointer(0, 3, GL_FLOAT, GL_FALSE, 3 * sizeof(float), (void*)0);
	glEnableVertexAttribArray(0);
}

#pragma endregion


void Render()
{
	glClearColor(0.5, 0.5, 0.5, 1);
	glClear(GL_COLOR_BUFFER_BIT);

	glBindVertexArray(VAO);
	glDrawArrays(GL_POINTS, 0, count);
}

int main()
{
	int x1, y1, x2, y2;
	std::cin >> x1 >> y1 >> x2 >> y2;

	InitializeWindow();

	DDA(x1, y1, x2, y2);
    Bresenham(x1, y1, x2, y2);

	InitializeVertex();

	while (!glfwWindowShouldClose(window))
	{
		ProcessInput(window);

		Render();

		glfwSwapBuffers(window);
		glfwPollEvents();
	}

	glfwTerminate();
	return 0;
}