基础图形绘制-圆

中点画圆

首先，我们考虑画圆心在 (0,0)(0,0) 的圆，其它情况仅需要平移即可。

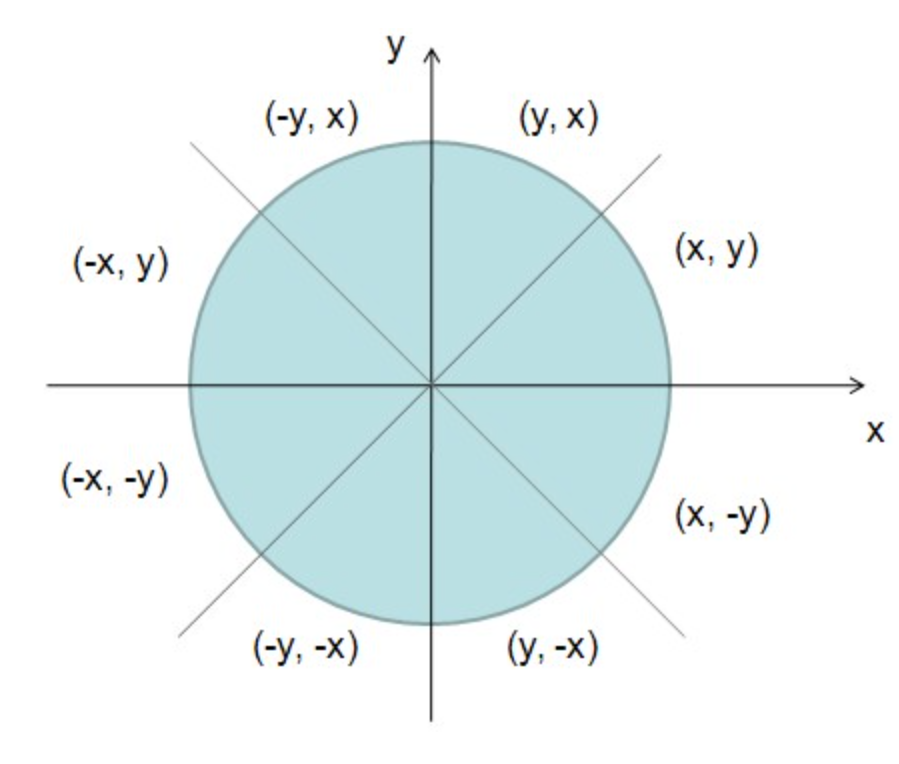
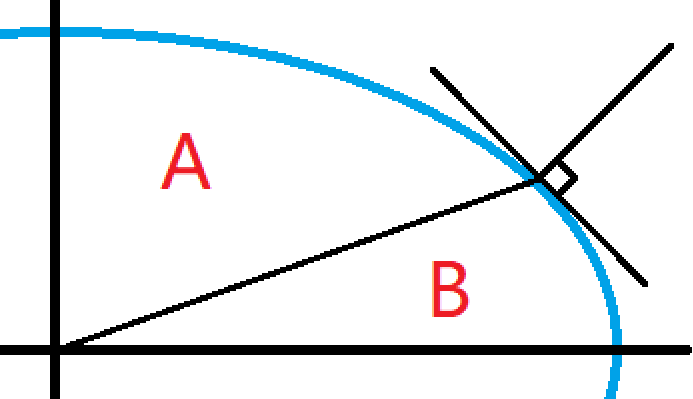
根据圆的对称性，我们只需要画出第一象限的 18\frac{1}{8} 的圆弧，即可通过对称画出整个圆。

image-20210925155553037

圆心在 (0,0)(0,0) ，半径为 RR 的圆的隐函数为：F(x,y)=x2+y2−R2=0F(x,y)=x^2+y^2-R^2=0，代入各点，有：

  1. 当 F(x,y)=x2+y2−R2=0F(x,y)=x^2+y^2-R^2=0 时，点在圆上；
  2. 当 F(x,y)=x2+y2−R2>0F(x,y)=x^2+y^2-R^2 \gt 0 时，点在圆外；
  3. 当 F(x,y)=x2+y2−R2<0F(x,y)=x^2+y^2-R^2 \lt 0 时，点在圆内。

考虑画右上方的 18\frac{1}{8} 圆弧，假设当前点在 (x,y)(x,y) ，考虑下一个点选择 (x+1,y)(x+1,y) 还是 (x+1,y−1)(x+1,y-1) 。

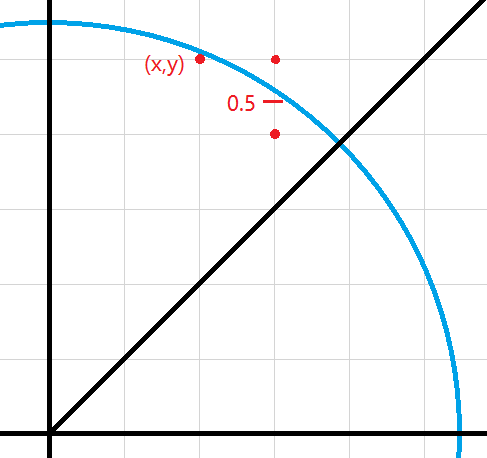
image-20210925161813173

下一个点显然是选择 离圆弧更近的点 ，我们可以通过判断 (x+1,y−0.5)(x+1,y-0.5) 在 圆内 还是 圆外，来判断 (x+1,y)(x+1,y) 、 (x+1,y−1)(x+1,y-1) 哪个离圆弧更近（需要注意的是：如果 (x+1,y−0.5)(x+1,y-0.5) 恰好在圆上，算法选择 (x+1,y−1)(x+1,y-1) 来作为下一个点）。

也就是说，对于 (x,y)(x,y) ，我们判断

d=F(x+1,y−0.5)=(x+1)2+(y−0.5)2−R2=x2+y2+2x−y+1.25−R2\begin{aligned} d &= F(x+1,y-0.5)\\ &= (x+1)^2+(y-0.5)^2-R^2\\ &= x^2+y^2+2x-y+1.25-R^2 \end{aligned}

的值，来判断下一个点的选择情况。

  1. 若 d<0d \lt 0，选择 (x+1,y)(x+1,y) 作为下一个点。
    此时，判断 (x+1,y)(x+1,y) 的下一个点的判断值为：

    d′=F((x+1)+1,(y)−0.5)=F(x+2,y−0.5)=(x+2)2+(y−0.5)2−R2=x2+y2+4x−y+4.25−R2=(x2+y2+2x−y+1.25−R2)+2x+3=d+2x+3\begin{aligned} d' &= F((x+1)+1,(y)-0.5)\\ &= F(x+2,y-0.5)\\ &= (x+2)^2+(y-0.5)^2-R^2\\ &= x^2+y^2+4x-y+4.25-R^2\\ &= (x^2+y^2+2x-y+1.25-R^2)+2x+3\\ &= d+2x+3 \end{aligned}

  2. 若 d≥0d \ge 0，选择 (x+1,y−1)(x+1,y-1) 作为下一个点。
    此时，判断 (x+1,y−1)(x+1,y-1) 的下一个点的判断值为：

    d′=F((x+1)+1,(y−1)−0.5)=F(x+2,y−1.5)=(x+2)2+(y−1.5)2−R2=x2+y2+4x−3y+6.25−R2=(x2+y2+2x−y+1.25−R2)+2x−2y+5=d+2x−2y+5\begin{aligned} d' &= F((x+1)+1,(y-1)-0.5)\\ &= F(x+2,y-1.5)\\ &= (x+2)^2+(y-1.5)^2-R^2\\ &= x^2+y^2+4x-3y+6.25-R^2\\ &= (x^2+y^2+2x-y+1.25-R^2)+2x-2y+5\\ &= d+2x-2y+5 \end{aligned}

这样我们就可以递推 dd 的值，不断选择点并更新判断值。

同时考虑初始点 (0,R)(0,R) ，显然有：

d0=F(0+1,R−0.5)=1+(R−0.5)2−R2=1.25−R\begin{aligned} d_0 &= F(0+1,R-0.5)\\ &= 1+(R-0.5)^2-R^2\\ &= 1.25-R \end{aligned}

这样，我们就可以画出基础的圆。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
static int dx[] = { 1, 1, -1, -1 };
static int dy[] = { 1, -1, 1, -1 };

static void Normalize(float& x, float& y)
{
	x = (x - (SCR_WIDTH / 2)) / (SCR_WIDTH / 2);
	y = (y - (SCR_HEIGHT / 2)) / (SCR_HEIGHT / 2);
}

static void MiddlePoint(int x0, int y0, int R)
{
	int x = 0, y = R;
    double d = 1.25 - R;
	while (x < y)
	{
		if (d < 0) d = d + 2 * x + 3;
		else y--, d = d + 2 * x - 2 * y + 5;
		
		x++;

		for (int i = 0; i < 4; i++)
		{
			vertices[count * 3] = x * dx[i] + x0, vertices[count * 3 + 1] = y * dy[i] + y0;
			Normalize(vertices[count * 3], vertices[count * 3 + 1]), count++;

			vertices[count * 3] = y * dx[i] + x0, vertices[count * 3 + 1] = x * dy[i] + y0;
			Normalize(vertices[count * 3], vertices[count * 3 + 1]), count++;
		}
	}
}

Bresenham

Bresenham 算法是对 中点画圆 算法的改进。

我们发现 中点画圆 算法中 dd 的值涉及到过多的浮点数运算，在经过各种改进后，我们考虑对算法做一些数值上的近似。选择了新的方案，也被称为 Bresenham 算法：

我们先将所有的关于 dd 的运算扩大两倍，然后将 d=2×(1.25−R)=2.5−2Rd=2 \times (1.25-R) =2.5-2R 改为 3−2R3-2R。也就是说：

  1. dd 的初值为 3−2R3-2R ；
  2. d<0d \lt 0 时，d′=d+4x+6d'=d+4x+6；
  3. d≥0d \ge 0 时，d′=d+4x−4y+10d'=d+4x-4y+10。

可以发现效果较好的同时消除了浮点运算。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
static int dx[] = { 1, 1, -1, -1 };
static int dy[] = { 1, -1, 1, -1 };

static void Normalize(float& x, float& y)
{
	x = (x - (SCR_WIDTH / 2)) / (SCR_WIDTH / 2);
	y = (y - (SCR_HEIGHT / 2)) / (SCR_HEIGHT / 2);
}

static void Bresenham(int x0, int y0, int R)
{
	int x = 0, y = R, d = 3 - 2 * R;
	while (x < y)
	{
		if (d < 0) d = d + 4 * x + 6;
		else y--, d = d + 4 * x - 4 * y + 10;

		x++;

		for (int i = 0; i < 4; i++)
		{
			vertices[count * 3] = x * dx[i] + x0, vertices[count * 3 + 1] = y * dy[i] + y0;
			Normalize(vertices[count * 3], vertices[count * 3 + 1]), count++;

			vertices[count * 3] = y * dx[i] + x0, vertices[count * 3 + 1] = x * dy[i] + y0;
			Normalize(vertices[count * 3], vertices[count * 3 + 1]), count++;
		}
	}
}

OpenGL 完整代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
#define GLEW_STATIC
#include <GL/glew.h>
#include <GL/GL.h>
#include <GLFW/glfw3.h>

#include <iostream>

#pragma region Setting

static GLFWwindow* window;
const unsigned int SCR_WIDTH = 800;
const unsigned int SCR_HEIGHT = 600;
const unsigned int MAX_COUNT = 800 * 600;

static void InitializeWindow()
{
	glfwInit();
	glfwWindowHint(GLFW_CONTEXT_VERSION_MAJOR, 3);
	glfwWindowHint(GLFW_CONTEXT_VERSION_MINOR, 3);
	glfwWindowHint(GLFW_OPENGL_PROFILE, GLFW_OPENGL_CORE_PROFILE);

	window = glfwCreateWindow(SCR_WIDTH, SCR_HEIGHT, "Test", NULL, NULL);
	glfwMakeContextCurrent(window);
	glfwSetFramebufferSizeCallback(window, [](GLFWwindow* window, int width, int height){ glViewport(0, 0, width, height); });


	glewExperimental = GL_TRUE;
	glewInit();

}

static void ProcessInput(GLFWwindow* window)
{
	if (glfwGetKey(window, GLFW_KEY_ESCAPE) == GLFW_PRESS)
		glfwSetWindowShouldClose(window, true);
}
#pragma endregion


#pragma region InitializeVertex

static float vertices[MAX_COUNT * 3];
static unsigned int VAO, VBO;
static unsigned int count = 0;

static int dx[] = { 1, 1, -1, -1 };
static int dy[] = { 1, -1, 1, -1 };

static void Normalize(float& x, float& y)
{
	x = (x - (SCR_WIDTH / 2)) / (SCR_WIDTH / 2);
	y = (y - (SCR_HEIGHT / 2)) / (SCR_HEIGHT / 2);
}

static void MiddlePoint(int x0, int y0, int R)
{
	int x = 0, y = R, d = 1.25 - R;
	while (x < y)
	{
		if (d < 0) d = d + 2 * x + 3;
		else y--, d = d + 2 * x - 2 * y + 5;
		
		x++;

		for (int i = 0; i < 4; i++)
		{
			vertices[count * 3] = x * dx[i] + x0, vertices[count * 3 + 1] = y * dy[i] + y0;
			Normalize(vertices[count * 3], vertices[count * 3 + 1]), count++;

			vertices[count * 3] = y * dx[i] + x0, vertices[count * 3 + 1] = x * dy[i] + y0;
			Normalize(vertices[count * 3], vertices[count * 3 + 1]), count++;
		}
	}
}

static void Bresenham(int x0, int y0, int R)
{
	int x = 0, y = R, d = 3 - 2 * R;
	while (x < y)
	{
		if (d < 0) d = d + 4 * x + 6;
		else y--, d = d + 4 * x - 4 * y + 10;

		x++;

		for (int i = 0; i < 4; i++)
		{
			vertices[count * 3] = x * dx[i] + x0, vertices[count * 3 + 1] = y * dy[i] + y0;
			Normalize(vertices[count * 3], vertices[count * 3 + 1]), count++;

			vertices[count * 3] = y * dx[i] + x0, vertices[count * 3 + 1] = x * dy[i] + y0;
			Normalize(vertices[count * 3], vertices[count * 3 + 1]), count++;
		}
	}
}

static void InitializeVertex()
{
	// Generate
	glGenVertexArrays(1, &VAO);
	glGenBuffers(1, &VBO);

	// Bind
	glBindVertexArray(VAO);
	glBindBuffer(GL_ARRAY_BUFFER, VBO);

	glBufferData(GL_ARRAY_BUFFER, sizeof(vertices), vertices, GL_STATIC_DRAW);

	glVertexAttribPointer(0, 3, GL_FLOAT, GL_FALSE, 3 * sizeof(float), (void*)0);
	glEnableVertexAttribArray(0);
}

#pragma endregion


void Render()
{
	glClearColor(0.5, 0.5, 0.5, 1);
	glClear(GL_COLOR_BUFFER_BIT);

	glBindVertexArray(VAO);
	glDrawArrays(GL_POINTS, 0, count);
}

int main()
{
	int x0, y0, R;
	std::cin >> x0 >> y0 >> R;

	InitializeWindow();

	MiddlePoint(x0, y0, R);
	Bresenham(x0, y0, R);

	InitializeVertex();

	while (!glfwWindowShouldClose(window))
	{
		ProcessInput(window);

		Render();

		glfwSwapBuffers(window);
		glfwPollEvents();
	}

	glfwTerminate();
	return 0;
}