骨骼动画原理

基础知识

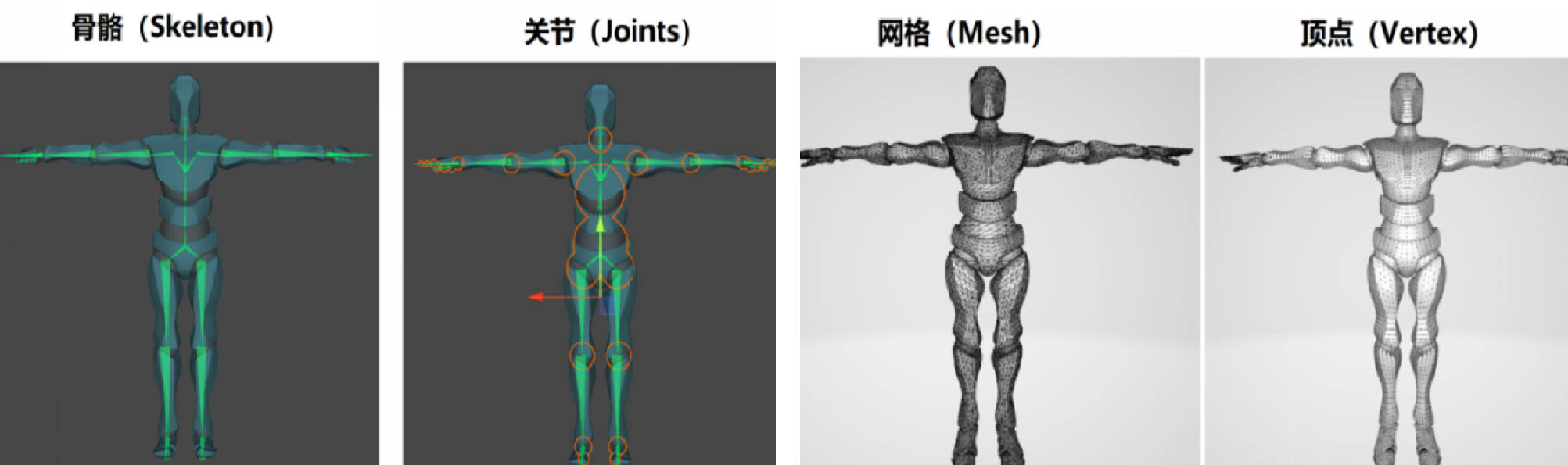
骨骼动画（Skeletal Animation） 是模型动画中的一种，通过改变骨骼的朝向和位置来为 模型 生成动画。

模型（Model）由一个个三角面组成，这种三角面也被称为 网格（Mesh），网格上有一个个 顶点（Vertex） 。

对应在骨骼动画中， 网格（Mesh） 也被称作 皮肤（Skin）；骨骼之间的连接处称作 关节（Joints），骨骼可以绕着 关节 旋转。

骨骼动画的制作，我们一般先进行 蒙皮 ，然后运动时根据提前制作好的 关键帧 与在两个关键帧之间的 插值 进行 姿态调整 生成动画。

image-20211127035412971

蒙皮

基础知识

对于两脚兽，一般使用 T-Pose 进行蒙皮，因为大部分姿势不会偏离它太大。

蒙皮 就是将 网格（Mesh） 的 顶点（Vertex） 给 绑定 在骨骼上，骨骼动画的本质就是用 骨骼 来操控 Mesh 动起来，Mesh 动起来的本质是 顶点 位置的改变。

一个 顶点 可能被多个 骨骼 影响（大部分情况一个顶点只会被一个骨骼影响，但是比如接近关节的顶点，单纯由一个骨骼影响可能会出现缝隙）。

确定被影响的方案就要使用 线性混合蒙皮（Linear Blend Skinning） 技术。

线性混合蒙皮

每个骨骼上会储存一个 变换矩阵（变换矩阵就是从 关节坐标系 到 世界坐标系 的 平移、旋转、缩放 矩阵的乘积，关节坐标系是以某个关节为原点的坐标系）

我们假设对这个顶点有影响的 骨骼 i 的 权重 为 w[i] 、变换矩阵为 M[i]、在 T-Pose 下的坐标为 V，那最后混合后的世界坐标 就为 sum(V * w[i] * M[i])，其中所有对其有影响的骨骼的权重之和为 1 。（其实这个公式就是按各个骨骼的权重比例转换，实际上是对每个骨骼的变换矩阵进行插值）

现在我们有了这个式子，需要的就是知道如何获得 变换矩阵，这就需要用到 正向动力学（Forward Kinematics） 了。

正向动力学

控制了关节的坐标，也就控制了骨骼、控制了模型。

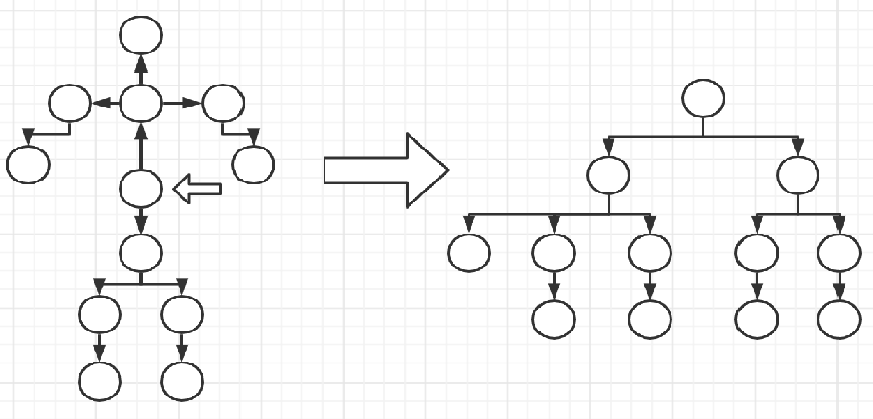
关节可以构成一棵树（一般两脚兽以 盆骨 为根节点），每个节点存储了 相对父节点 的变换矩阵（我们可以叫它 小变换矩阵）。

这样，一个父节点移动的时候，可以带动子节点一起移动。

image-20211127042112070

我们有了每个节点 相对父节点 的 小变换矩阵，从 关节坐标系 到 世界坐标系 的最终 变换矩阵 就由这一个个小变换矩阵累积获得，这个求解最终 变换矩阵 过程也就是 正向动力学 的本质。

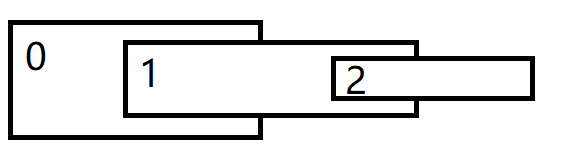
实际上，每个节点的这个最终 变换矩阵 也就是从 根节点 到 该节点 路径上，每个 小变换矩阵 的乘积。

image-20211127043125618

设骨骼 i 的 小变换矩阵 为 m[i]，特别的，根节点的变换矩阵设为 O，那显然对上图：M[0] = O、M[1] = m[1]* O、M[2] = m[2] * m[1] * O = M[1] * O，显然可以通过在树上进行一次遍历求得。

求解这个问题，这就是 正向动力学 了（一看就很 正向，从根节点 正向 往下走到叶节点）

姿态调整

基础知识

动画师编辑骨骼进行若干姿态的调整，在 关键帧 中我们直接手动调整姿态。

在非关键帧（两个关键帧之间的 插值 得到的）动画，也会有姿态的变换。

如何进行姿态的调整有两种方案：

  1. 对 变换矩阵 进行插值，需要用到 正向动力学（Forward Kinematics）。
  2. 对部分 关节坐标 进行插值，然后逆推所有坐标，需要用到 逆向动力学（Inverse Kinematics）

逆向动力学

对于关节树，给定末端的 关节坐标 ，怎么获得每个关节的坐标，从下往上 逆向 求解，就是 逆向动力学 的本质。

逆向动力学的解决方案一般是 CCD（Cyclic Coordinate Descent） 或 CAA（Circular Alignment Algorithm） 等。

CCD（循环坐标下降算法）

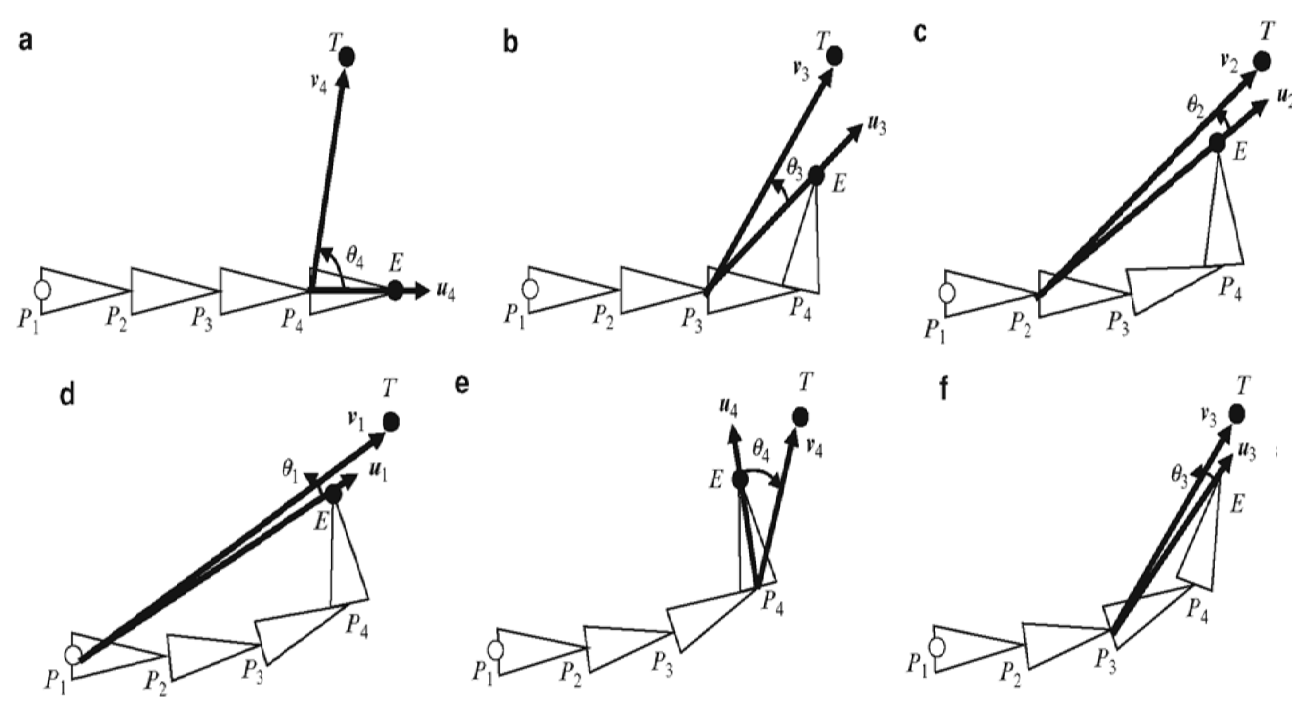
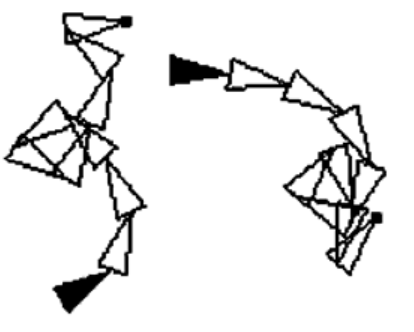
CCD 在关节链的上执行一系列旋转，从最后一个链节开始，每次尝试将 末端 移近 目标坐标，采用迭代的方式逐渐处理。

image-20211127050602039

CCD 算法也有不足之处：

  1. 一组关节的物理系统一般有 关节角度约束 等物理限制，在解决 逆向动力学 的时候需要考虑到这些限制。CCD 算法可以生成可能 违反关节角度约束 的大角度旋转。

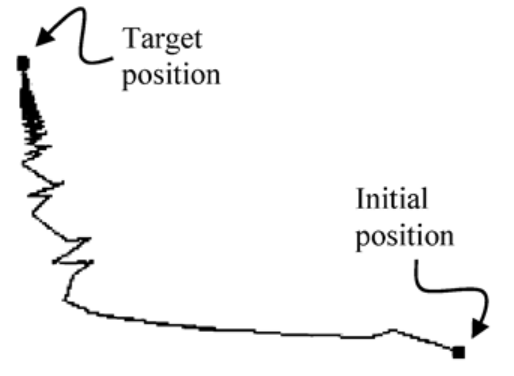
  2. 在某些情况下，特别是当靠近目标坐标时，CCD 算法会导致一条链形成循环 与自身相交。

image-20211127051144869

  1. 在某些情况下，CCD 可能会进行大量迭代，导致末端缓慢的 锯齿形运动。

image-20211127051220872

CAA（Circular Alignment Algorithm） 可以克服这些缺点。

CAA（圆形对齐算法）

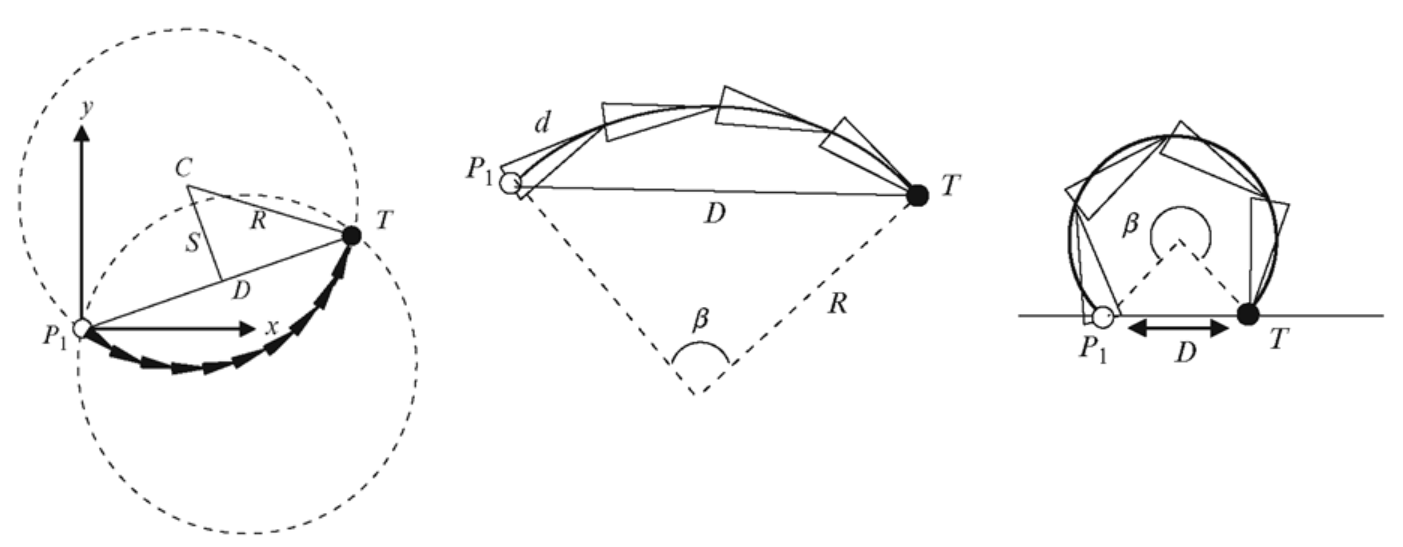
CCA 给定的关节链沿 基点 和 可到达的目标位置 之间的若干圆弧。通过这些圆弧，计算可接受范围内的关节角度，实现 逆向动力学。

image-20211127051811031

CAA 要求所有圆弧具有相同的长度，以便计算。

CAA 在包含圆弧的 基点 和 目标坐标 的二维平面上工作。因此，一般的三维问题会被简化为二维问题，所有关节链都被限制为在单个平面上移动。

插值

让非关键帧动画 平滑且连续 需要用到插值；空间变换有三种操作：平移、旋转、缩放。

其中，平移、缩放，显然可以平移矩阵、缩放矩阵直接进行 线性插值，但是旋转显然不行，旋转是在一个球面上移动，我们需要用到 四元数 进行 球面线性插值 。

参考

GPU Skinning：骨骼动画原理：https://zhuanlan.zhihu.com/p/126293705

浅谈骨骼动画技术原理：https://zhuanlan.zhihu.com/p/431446337

Kinematics (Advanced Methods in Computer Graphics) ：http://what-when-how.com/advanced-methods-in-computer-graphics/kinematics-advanced-methods-in-computer-graphics-part-4/